“I’ve got some amazing project-based learning ideas that will light a fire under my students. Can’t wait to do them…after testing!” If this sounds familiar, then you have firsthand experience with the pressure to “cover” ungodly amounts of material before high-stakes exams. Too often, this pressure creates a joyless experience for teachers and students alike. But what if it didn’t have to be this way?
Request a quote for thinkLaw’s award-winning curriculum now to use our engaging and rigorous real-life legal cases to help teachers give students the essential critical thinking skills they need for success.
What if you could engage students in rigorous and engaging learning activities AND ensure they were prepared for exams that have become increasingly challenging over time? It turns out that hacking test prep with critical thinking is not only feasible, but necessary. Because let’s be real: if there was such a thing as “teaching to the test,” we would’ve cracked that code by now. Whether your state uses the PARCC, SBAC, STAAR, AzMerit, SOL (quite the choice of initials there, Virginia) or a different assessment, rote memorization and spoon-fed learning are not going to prepare students for success on these exams. Here’s an example of why drill-and-kill doesn’t work:
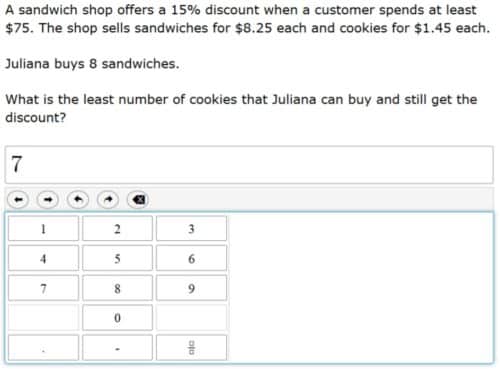
This question from a Grade 7 2018 AzMerit released item (Arizona) is a perfect example of why “teaching to the test” is impossible. To get this question right, a student needs to understand the purpose of five different numbers, avoid being fooled by the 15% figure which is not relevant to the problem, understand how inequalities are set up, know how to multiple decimals, subtract whole numbers, and divide decimals. And if that isn’t enough, the student must recognize that Juliana can’t buy 6.2 cookies, so she will have to buy 7 in order to get the discount.
This means that as common as drill-and-kill worksheets and Jeopardy-style review games are, these simply will not cut it. Students need critical thinking to apply their knowledge and exercise tons of logical reasoning to work through tricky multi-step and multiple-choice questions. Here are three strategies you can use to “hack” test prep with critical thinking:
1. Guess-timation in Complete Sentences
There is A LOT going on in this problem:
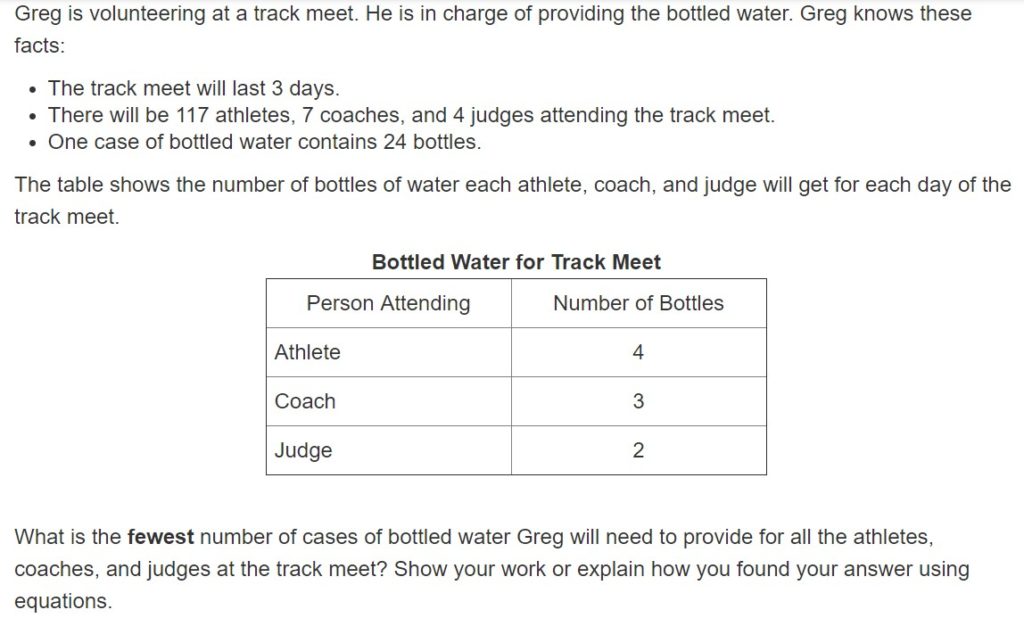
To get students set up with success and with a contextual understanding to help them make effective predictions and inferences for a reasonable answer, we’ve got to start with the ending! If students highlight the question and prepare an answer like this:
_____ is the fewest number of cases of bottled water Greg will need to provide for all the athletes, coaches, and judges at the track meet.
Now they are Greg, and they are looking for the “fewest” number of “cases” (not bottles, but cases) and they know we are counting these up for the number of athletes, coaches, and judges. And if they round the number of athletes to 120 times 3 bottles each they get 480. Rounding 7 coaches times 3 bottles each to 20 gets us to 500. And 4 judges times two per judge brings us to 510. Keep it simple, and just stay at 500, divide by 25 (because who estimates using the number 24), and we now the answer should be somewhere in the neighborhood of 20. Training students to step into the shoes of the person with the strategy of guess-timating in complete sentences helps them develop much more reasonable answers.
2. Pulp Fictionize readings:
I’m convinced that Pulp Fiction would be one of the most “blah” movies ever if the story was told in order. But by putting together a movie with an odd chronological order, the audience is forced to decode and make sense of the story in a way that unleashes all sorts of higher order thinking. With standardized ELA/Reading exams constantly asking students to analyze numbered paragraphs with common questions about the main idea, setting, purpose, the meaning of vocabulary words, and even questions asking them to create their own chronology like the item below, try channeling your students’ inner Quenton Tarantino (minus the gory violence).

3. Watching out for Choice A “Gotchas”
Developing a healthy sense of skepticism is a powerful component of critical thinking. So take a look at this problem to see why this trait is so important to avoid making mistakes due to a common technique used by test makers:

Grade 5 Math PARRC
As a former “I must be the first kid done” student, I initially rushed through this problem. I saw the problem was asking about meat loaf and ground beef, saw 5 meat loaves, 9 pounds, and thought, “easy!” That’s just 5/9, which is ½. Then I realized that was choice A. I then asked myself, “self…are you about to fall for the Choice A Gotcha? Nope!” Test makers often design questions that require students to look at a variety of answer choices with a trick answer for choice A, specifically targeting fast test takers like myself. When students realize the way these tests try to fool you, they can’t help but to develop the type of skepticism that comes from feeling some type of way about test takers that try to catch them slipping.
4. Metacognition and Mistake Analysis
Metacognition, or thinking about your own thinking, is a highly-effective strategy to hack standardized exams. Take a look at this example:

Grade 4 2018 Released Question, STAAR (Texas)
Instead of just asking students to select the right answer in this passage about the history of Wrigley’s gum, ask them to analyze the thinking of a student who selected each incorrect answer based on textual evidence. The student who selected choice F might be thinking about actually buying gum and recognizing that gum has become more expensive over the years, even though that isn’t what this sentence is really about. The choice H student might be thinking about the fact that gum is typically placed on check-out counters because people forget, so that is also a true statement. And the choice J student might be looking at the two mentions of different flavors and conclude that this was really just about the increase in gum diversity.
This also works in math:
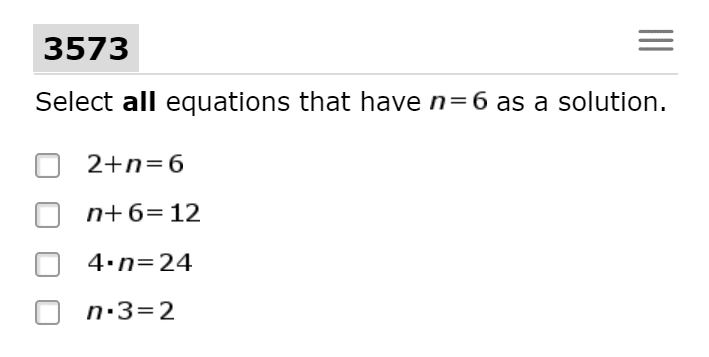
Grade 6 SBAC
The first one is in the Choice A Gotcha family because the equation is equal to 6 even though n = 4 would actually be the solution. And a student checking the last example confused division and multiplication, because although 6 divided by 3 is two, n would have be 2/3 for n times 3 to equal 2.
5. Teach to the Test Format
A common source of student and teacher frustration with standardized exams is the need to master not just the test content, but the test format. Between the mechanics of tests that are increasing computerized and the ever-evolving format of test questions, it can often seem like these tests are measuring the ability to understand test logistics just as much as the questions themselves. And with thinkLaw leading a critical thinking revolution in 16 states, these challenges are multiplied for students who end up moving to states with a different test structure.
These are valid critiques. But considering the world we are preparing our students for, where they will need to solve problems we haven’t identified yet using technologies that haven’t been created yet in career fields that do not currently exist, there is inherent value in equipping our students with the adaptability needed to respond to questions in lots of unfamiliar formats. Learning how to learn is a core aspect of 21stt century readiness, so choosing between critical thinking and adherence to test questions is a false choice.









Leave a Reply